Number Sense

Students who develop number sense have a range of mathematical strategies at their disposal. They know when to use them and how to adapt them to meet different situations. They can also utilise mathematical reasoning to solve problems and communicate their process and answer clearly. 

By utilising The Learner First’s recallNreason activities, students in Room 8 have regular opportunities to develop their number fluency, consolidate known facts and apply them with speed and efficiency to a range of problems and games.

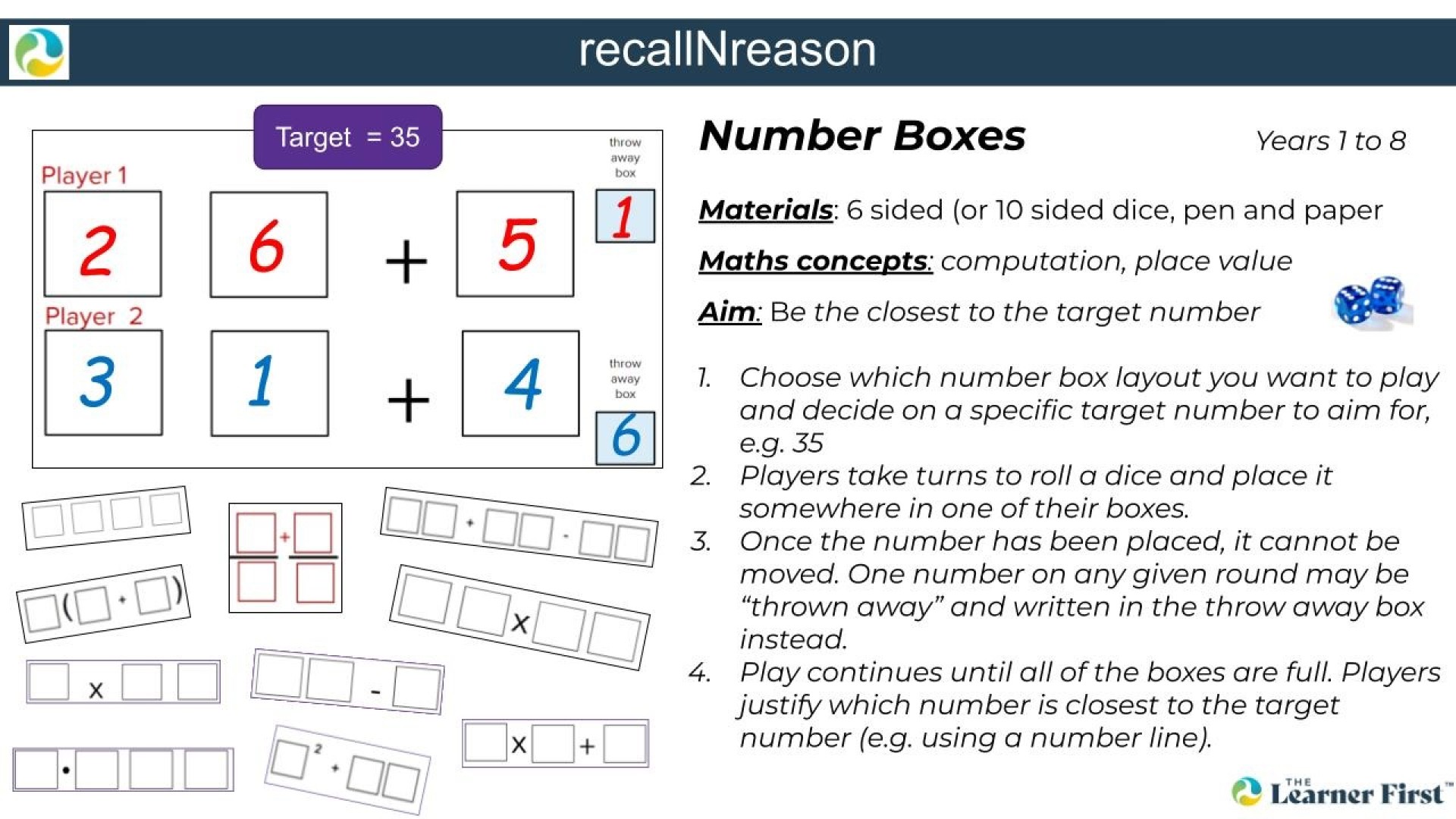
Number Boxes

This game is designed to develop a learner's ability to manipulate numbers in an addition calculation in order to reach a desired target number. 

A key part of this game is for students to understand which digits to put in the tens and ones column and which digit to discard into the throw away box. After each throw of the dice, students have to explain to their learning buddy why they put each digit either into the tens, ones or throw away box.

Whilst trying to find the largest number, Rylen explained why he discarded the digit 1:

I know that 1 is the smallest possible digit so I had a good chance of throwing a bigger number. So I decided to throw the number 1 away.

Having placed the digit 6 in the tens column, Hazel explained her reasoning to Nova:

Six is the highest number I can throw on a die so I know that it has to go in the tens column.

When asked what digit Nova needed to throw in order to beat Hazel’s score of 68, she responded:

I know I can’t beat her because the highest I can get is 68, so if I don’t roll a 6 I know that I’ve lost

Whilst trying to reach the target number of 15, Wesley had just thrown a 6. He decided to place this in the ones column and explained his reason why:

I know I can’t put the 6 in the tens column because that will give me a number in the sixties and I know I need a 1 in my tens column to get nearest to 15.  

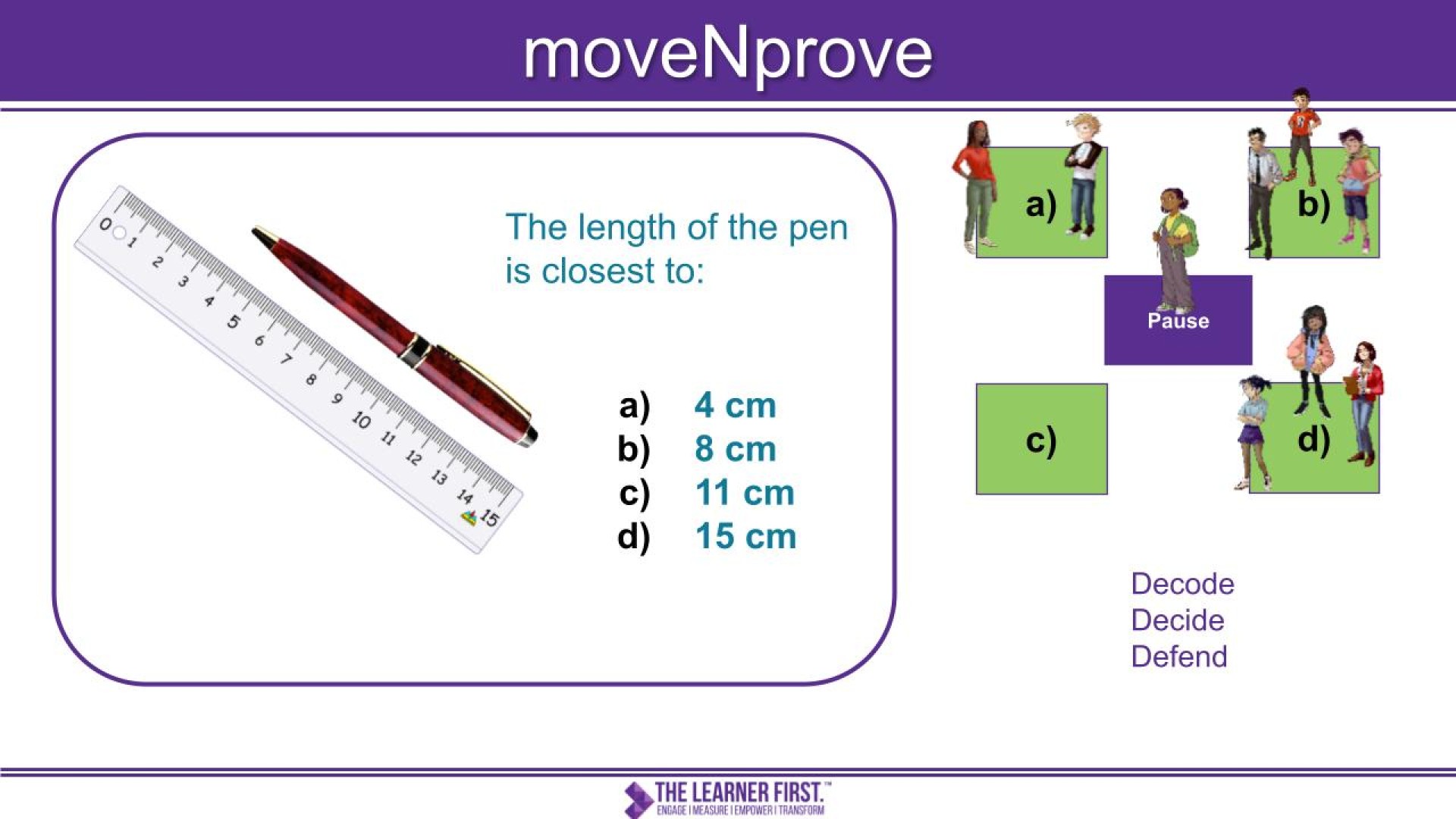
MoveNprove’s provides learners an opportunity to calculate the answer to an unfamiliar word-problem, discuss their answer with a learning buddy, and verbally reason with their peers.

Once they have been given time to think, student’s have the option to move to the four corners of the room (each corner representing a different answer). Each group must then choose a representative to defend and prove their position. In this example, the majority of students chose option c whilst a small number selected option d.

In order to defend his group's position, Kyan stated:

It must be d because the end of the pen is in-line with 15cm. When you use a ruler, you have to look at where the object ends and the pen ends at 15cm. 

To defend the position of those students who chose option c, Tom responded by saying:

I disagree with Kyan because the pen doesn’t start at 0cm. It starts at 4cm so we have to do a subtraction calculation.

To promote more than one student speaking, I asked another student to explain how they calculated the answer. Hendrick explained his process:

I agree with Tom. To work out my answer, I did 15 - 4 and I know the answer is 11. So the pen must be 11cm long. 

In addition to explaining why they think their answer is correct, student’s are also given the opportunity to disprove another answer. When asked who can explain why answer a is incorrect, Storm stated:

It can’t be 4cm because the pen only just fits onto a 15cm ruler. So it can’t be a length as small as 4cm.

When asked what mistake a student could have made by choosing 4cm, Hazel stated:

They probably looked at the ruler and started at the 0cm because that is what we are taught to do. They then stopped at 4cm because that is when the pen started. But all they measured was the gap on the ruler.